Pythonで水文水理解析をやってみる。[Chapter 3]
水文解析の基本_1 [Chapter 2] に引き続き、Precipitation(降雨)について学んでいきます。
このTutorialは、Python in Hydrologyを使って、Pythonの基本的な勉強とPythonで水文水理解析の勉強していきます。
ただし、本Blog中の専門用語の翻訳、source code等に関しては、あくまでも参考としてください。なにがあっても責任とれませんので。
そこんところ、ヨロシク~~!!
水文解析の基本
本章の中の問題は、chowによって「応用水文学」というタイトルの本からのものです。また、それらの詳細な記述については、「応用水文学」の本を参照してください。このtutorialは、水文学の中で一般的な方程式を含んでいます。
水文学の基本として、まずは、以下の7項目について、Pythonを使って学んでいきます。
-
Water Vapor(水蒸気)
-
Precipitation(降雨) →今回はここ
-
Rainfall(降水量)
-
Evaporation(蒸発散)
-
Infiltration(浸透)
-
Surface water(表面流)
-
River Routing–Muskingum method(マスキンガム法による河道流)
Precipitation(降雨)
Rainfall(降水量)については次章で説明します。
ここでは、Precipitation(降雨)の終末速度(terminal velocity)について計算してみます。終末速度とは、雨粒が地上に落下して地上に到達する際の速度のことで、
の式で表されます。
ここで、gは重力加速度, Dは雨粒の直径, ρwは水の密度, ρaは大気の密度, そしてCdは抵抗係数(drag coefficient)です。ストークスの抵抗則(Stoke’s law)によれば、雨粒の直径が0.1mmよりも小さい場合は、抵抗係数(drag coefficient)は(Cd = 24/Re)として計算することができます。Reは、ρaVD/µaで計算されるレイノルズ数(Reynold number)です。
ここで、以下の仮定でVtを計算してみましょう。
Reのレイノルズ数(Reynold number)は5.0, 雨粒の直径は0.05 mm, そして(ρw = 998, ρa = 1.2)とします。
[python]
import numpy as np
Re = 5.0; rho_w = 998; rho_a = 1.2; g = 9.8; D = 0.05E-3
Cd = 24/Re
Vt = np.sqrt((4*g*D)/(3*Cd)*(rho_w/rho_a-1))
print (Vt)
[/python]
終末速度は、0.336248364997となります。
c:¥python_hydrology¥chapter4¥にterminal_velocity.pyと保存後、実行すると、
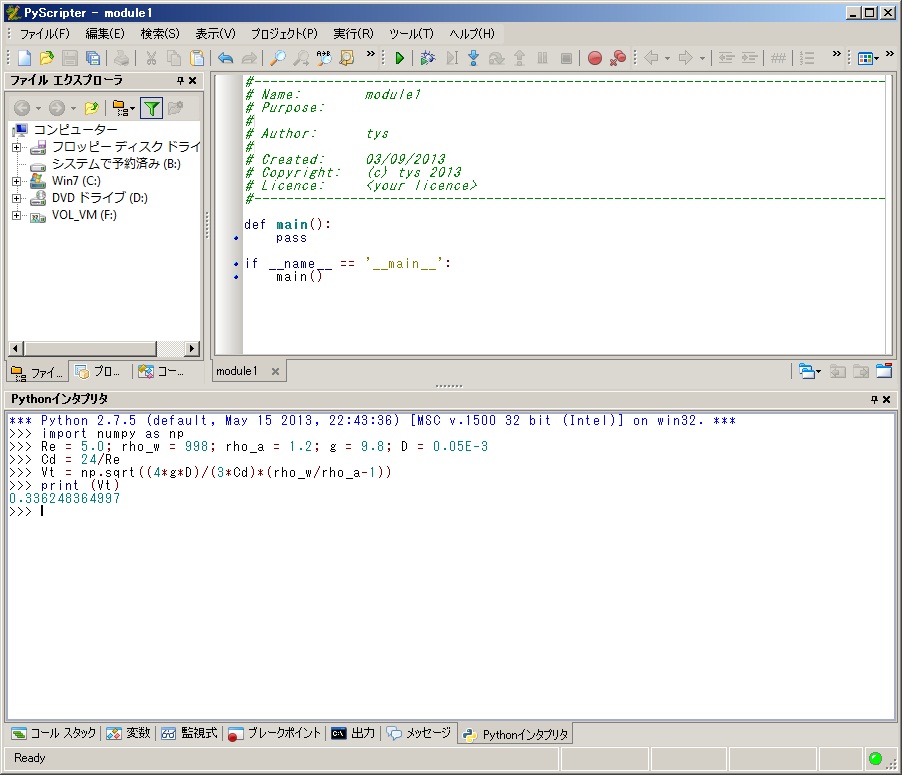
のように結果がインタープリタ画面に表示されます。
今回のまとめ
水文解析の基本_2 [Chapter 3]のPrecipitation(降雨)の終末速度(terminal velocity)について勉強しました。
次回は、Rainfall(降水量)について勉強していきます。
Python GeoSpatial TutorialではGISについてblogを書いていますので、GISに興味のある方はのぞいてみてください。
また、本Tutorialは、Python Scriptの基本的なことはある程度理解している前提で今後も話を進めていきます。また、誤字、脱字、spell間違いや翻訳の勘違いも多々出てくると考えられます。
特に英語から日本語への専門用語の翻訳については、プロではないので、「それは違うじゃん!!」とかいろんな意見をいただければと思います。

Comments are closed.